注：本篇适用于复习

方阵的特征值和特征向量

  1. 特征值与特征向量

    • 定义：设A是n阶方阵，如果存在数$\lambda$和n维非零向量X使关系式AX =$\lambda$X成立，则称数$\lambda$为方阵A的特征值;非零列向量X称为A对应于特征值$\lambda$的特征向量.

    • f($\lambda$)=|A-$\lambda$E|是$\lambda$的n次多项式，称为A的特征多项式.

    • f($\lambda$)=0即

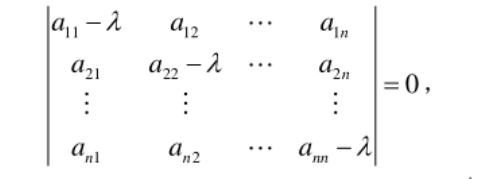
      是以$\lambda$为未知数的一元n次方程，称为A的特征方程，特征方程的根就是A的特征值.
      kX也是方阵A的特征向量，属于同一特征值的特征向量有无穷多个;反之，不同特征值对应的特征向量必不相同，即一个特征向量只能属于一个特征值.

    • 定理：设$\lambda$是方阵A的特征值，$\ p_1$, $\ p_2$, …, $\ p_s$是属于$\lambda$的特征向量，则$\ p_1$, $\ p_2$, …, $\ p_s$的任意非零线性组合仍是属于$\lambda$的特征向量.

  2. 特征值和特征向量的性质

    • 定理：设$\ \lambda1$, $\ \lambda_2$, …, $\ \lambda{n}$是n阶方阵A =$\ (a_{ij}$)的n个特征值，则有

      • $\stackrel{n}{\sum\limits{i=1}}\lambda_i$= $\stackrel{n}{\sum\limits{i=1}}a_{ii}$

      • $\stackrel{n}{\prod\limits_{i=1}}\lambda_i$ = |A|

      其中$\stackrel{n}{\sum\limits{i=1}}a{ii}$是A的主对角元之和，称为方阵A的迹，记作tr(A).

    • 定理： 设$\lambda$是方阵A的特征值，p是A的属于$\lambda$的任一特征向量，则有:

      1. $\forall$k∈R，k$\lambda$是kA的特征值，p是kA的属于k$\lambda$的特征向量;

      2. 对任意非负整数k，$\lambda^k$是A$^k$的特征值，p是A$^k$的属于$\lambda^k$的特征向量;

      3. 若$\varphi$(A)是A的m(m为任意非负整数)次多项式，即$\varphi$(A)= $\ a_0$E+$\ a_1$A, …, $\ a_m$A$^m$,则$\varphi$($\lambda$)是$\varphi$(A)的特征值，p 是$\varphi$(A)的属于$\varphi$($\lambda$)的特征向量;

      4. 若A可逆，则$\lambda$≠0，且$\frac{1}{\lambda}$是A$^{-1}$的特征值，p是A$^{-1}$的属于$\frac{1}{\lambda}$的特征向量;

      5. 若A可逆，$\frac{|A|}{\lambda}$则是A$^$的特征值，p是A$^$的属于$\frac{|A|}{\lambda}$的特征向量;

      6. $\lambda$也是A$^T$的特征值.

    • 定理：不同特征值对应的特征向量线性无关.

相似矩阵

  1. 相似矩阵的概念与性质

    • 定义：设A,B均是n阶方阵，如果存在n阶可逆矩阵P，满足P$^{-1}$AP = B ，则称A与B相似，或B是A的相似矩阵，记作A~B，可逆矩阵p称为把A相似变换为B的相似变换矩阵.(矩阵的相似关系是矩阵等价关系的特殊情形)

    • 性质：

      1. 反身性：A~A；

      2. 对称性：若A~B，则B~A；

      3. 传递性：若A~B，B~C，则A~C.

    • 定理：设A~B，变换阵为P，则

      1. $\forall$k∈R，kA ~kB，变换阵仍为P;

      2. 任意正整数k ，A$^k$~B$^k$，变换阵仍为P;

      3. $\varphi$(A)~$\varphi$(B)($\varphi$(·)为任意矩阵多项式)，变换阵仍为P;

      4. A$^T$~B$^T$，变换阵为(A$^T$)$^{-1}$;

      5. 若A可逆，则B也可逆，且A$^{-1}$~B$^{-1}$，A$^$~B$^$，变换阵均为P.

    • 定理（相似不变性）：设A~B，则

      1. R(A)=R(B);

      2. A与B有相同的特征值;

      3. |A|=|B|，tr(A)=tr(B).

    • 推论︰若A与对角阵$\Lambda$= diag($\lambda1$, $\lambda_2$, …, $\lambda{n}$)相似，则$\lambda1$, $\lambda_2$, …, $\lambda{n}$就是A的n个特征值.

  2. 矩阵的对角化

    • 定义：若存在可逆矩阵P和对角阵$\Lambda$= diag($\lambda1$, $\lambda_2$, …, $\lambda{n}$)，使P$^{-1}$AP = A成立，则称A可对角化，称$\Lambda$为A的相似标准形

    • 定理：n阶方阵A可对角化$\Longleftrightarrow$A有n个线性无关的特征向量.

    • 推论：若n阶方阵A有n个不同的特征值，则A一定可以对角化.

    • 定理：设n阶方阵A的所有互异特征值为$\lambda1$, $\lambda_2$, …, $\lambda{s}$对应重数依次为$\ n1$, $\ n_2$, …, $\ n{s}$则A可对角化当且仅当R(A-$\lambda_i$E)=$\ n-n_i$,i=1,…, s，即对应于A的每个特征值的线性无关的特征向量的个数恰好等于该特征值的重数.

实对称矩阵的对角化

  1. 实对称矩阵特征值与特征向量

    • 定理：实对称矩阵的特征值全是实数，也必有实特征向量.

    • 定理：实对称矩阵属于不同特征值的特征向量一定正交.

    • 定理：设A为n阶实对称矩阵，$\lambda_i$是A的$\ n_i$重特征值，则RA-$\lambda_i$E)=$\ n-n_i$，从而特征值$\lambda_i$恰有$\ n_i$个线性无关的特征向量.

  2. 正交矩阵

    • 定义：若n阶方阵A满足A$^T$A=E，则称A为正交矩阵，简称正交阵.

    • 定理：正交阵A具有以下性质：

      1. A$^{-1}$=A$^T$也是正交阵;

      2. |A|=±1;

      3. 若B也是正交阵，则AB也是正交阵;

      4. A的行（列）向量组构成R$^n$的一个标准正交基.

    • 定义： 若P为正交阵，则相似变换B=P$^{-1}$AP称为正交变换.

  3. 实对称矩阵的对角化

    • 定理：设A为n阶实对称阵,则必有正交矩阵P，使得P$^{-1}$AP=$\Lambda$,其中$\Lambda$是以A的n个特征值为对角元的对角阵，即实对称矩阵必可经过正交变换对角化.