向量的线性关系复习

注：本篇适用于复习

向量及其线性表示

n维向量：由n个数组成的有序数组(x1, x2, …, xn) 组成数都为实数→实向量
行向量&列向量（无特别说明，后面出现的一般指列向量）
零向量：向量的各个分量全为0
向量相等：当且仅当二者的所有分量对应相等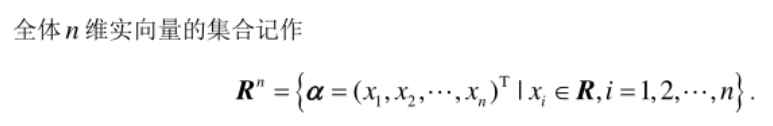
向量的线性运算：向量的加法和数乘

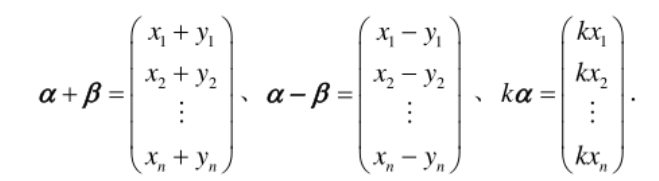
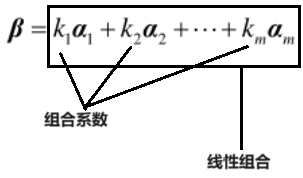称β可由向量组线性表示
- 定理：n维向量β可由n维向量组α$\ _1$, α$\ _2$, …, α$\ _m$线性表示$\Longleftrightarrow$线性方程组x$\ _1$α$\ _1$+x$\ _2$α$\ _2$+…+x$\ _m$ α$\ _m$=β有解$\Longleftrightarrow$方程组系数矩阵的秩R(A)= R($\overline{A}$)(增广矩阵的秩).

向量组的线性相关性

向量组的线性相关：若向量组A∶α$\ _1$, α$\ _2$, …, α$\ _m$(m≥2)中至少有一个向量可由其余m-1个向量线性表示，则称向量组A线性相关，否则称向量组A线性无关.
判断向量组线性相关or线性无关：
向量组α$\ _1$, α$\ _2$, …, α$\ _m$∈$R^n$线性相关$\Longleftrightarrow$存在一组不全为零的数$\ k_1$, $\ k_2$, …, $\ k_m$，使得$\ k_1α_1$+ $\ k_2α_2$+ …,+$\ k_mα_m$ = 0(零向量)
把上式中$\ k_1$, $\ k_2$, …, $\ k_m$看成未知元，即一个m元齐次线性方程组：
- 方程组有非零解$\Longleftrightarrow$方程组系数矩阵的秩R(A)<m$\Longleftrightarrow$n维向量组α$\ _1$, α$\ _2$, …, α$\ _m$线性相关；
- 方程组只有零解$\Longleftrightarrow$方程组系数矩阵的秩R(A)=m$\Longleftrightarrow$n维向量组α$\ _1$, α$\ _2$, …, α$\ _m$线性无关.
  - 对于只包含一个向量α的向量组，当α=0时是线性相关的，当α≠0时是线性无关的;
  - 对于包含两个向量的向量组，该向量组线性相关$\Longleftrightarrow$两向量的对应分量成比例，几何意义即两向量共线.
向量组线性相关的性质
1. 设向量组$\ α_1$, $\ α_2$, …, $\ α_m$线性无关，而向量组$\ α_1$, $\ α_2$, …, $\ α_m$,β线性相关，则β可以由向量组$\ α_1$, $\ α_2$, …, $\ α_m$线性表示，且表示式唯一.
  - 推论：若β可以由向量组$\ α_1$, $\ α_2$, …, $\ α_m$线性表示，则表示式唯一当且仅当向量组$\ α_1$, $\ α_2$, …, $\ α_m$线性无关.
2. 当向量组所含向量个数大于向量的维数时，则该组向量必线性相关.
  - 推论：n+1个n维向量一定线性相关.
- 把向量组的各个向量以同样的方式增加若干个分量得到的向量组叫接长向量组.把向量组的各个向量以同样的方式删除若干个分量得到的向量组叫截短向量组.
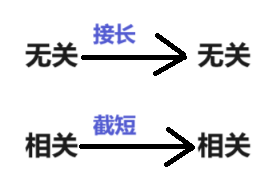  - 上图具有必然性，而反之则并不一定

向量组的秩

向量组的极大无关组
- 定义：给定n维向量组(I):$\ α_1$, $\ α_2$, …, $\ α_m$和(II)︰$\ β_1$, $\ β_2$, …, $\ β_m$如果(II)中的每一个向量都可以由(I)中的向量线性表示，称(II)可以由(I)线性表示．如果(II)可以由(I)线性表示，同时(I)也可以由(II)线性表示，则称(I)和(II)等价.
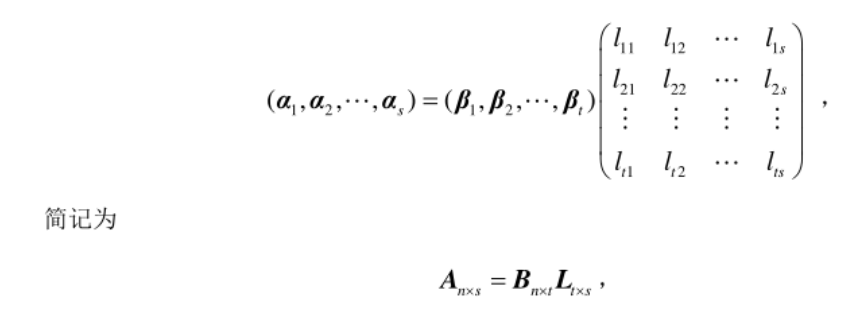其中A和B分别是由向量组(I)和(II)作为列向量组所组成的矩阵,L是由表示系数所组成的t ×s矩阵.同理，若向量组(II)也可以由 (I)线性表示，则有表示式$\ B{n×t} $ =$\ A{n×s} $ $\ L_{s×t} $成立，其中K是由表示系数所组成的s×t矩阵.
- 定义：设向量组$\ α_1$, $\ α_2$, …, $\ α_r$是$R^n$中向量组A的一个部分组（可以取整体），如果满足:
  (1）向量组$\ α_1$, $\ α_2$, …, $\ α_r$线性无关;
  (2）向量组A中的任意r+1个向量线性相关（如果A存在r+1个向量的话)，则称向量组$\ α_1$, $\ α_2$, …, $\ α_r$是向量组A的一个极大线性无关向量组（极大无关组).（全是零的向量组没有极大无关组）
  一般情况下，向量组的极大无关组不是唯一的．但同一个向量组的不同极大无关组包含的向量个数却是一样的．
向量组的秩
定义：向量组$\ α_1$, $\ α_2$, …, $\ α_m$的极大无关组所含向量的个数称为向量组$\ α_1$, $\ α_2$, …, $\ α_m$的秩，记作R($\ α_1$, $\ α_2$, …, $\ α_r$)·
- 定理：设n维向量组$\ β_1$, $\ β_2$, …, $\ β_m$线性无关，且$\ β_1$, $\ β_2$, …, $\ β_m$可由向量组$\ α_1$, $\ α_2$, …, $\ α_m$线性表示，则必有s≥t .（利用矩阵秩的性质)证明）
  - 推论：等价的线性无关向量组所含的向量个数必定相同（定理中的α和β交换条件可得t≥s则t=s）
- 定理：矩阵A的秩等于它的列向量组的秩(列秩)，也等于它的行向量组的秩(行秩).（矩阵初等变换不改变列秩与行秩）
- 定理：若向量组A可以由向量组B线性表示，则R(A)≤R(B).
  - 推论：若向量组A和向量组B等价，则R(A)=R(B).