注：本篇适用于复习

向量空间

  1. 向量空间及有关概念

    • 定义：设V为$R^n$的一个非空子集，如果V满足:
      (1)V对加法运算封闭，即V中任意两个向量的和向量仍在V中;
      (2)V对数乘运算封闭，即V中任意向量与任一实数的乘积仍在V中;
      则称V关于向量的线性运算构成实数域上的一个向量空间.

    • 定义：设$\ α_1$, $\ α_2$, …, $\ α_s$∈$R^n$，则可以验证由该向量组的所有线性组合得到的向量的集合U={xlx =$\ k_1α_1$+ $\ k_2α_2$+ …,+$\ k_sα_s$∈R}是一个向量空间。称U是由$\ α_1$, $\ α_2$, …, $\ α_s$所生成的子空间(或称为$\ α_1$, $\ α_2$, …, $\ α_s$的生成子空间)，记作
      U = Span($\ α_1$, $\ α_2$, …, $\ α_s$)，其中$\ α_1$, $\ α_2$, …, $\ α_s$称为U的生成元.

    • 设V是向量空间U的一个子集，如果V也是向量空间，则称V是U的子空间.

  2. 向量空间的基、维数和坐标

    • 定义：设V是一个向量空间，$\ α_1$, $\ α_2$, …, $\ α_r$是V中的一组向量，如果满足:
      (1)$\ α_1$, $\ α_2$, …, $\ α_r$线性无关;
      (2)V中的任一向量都可由$\ α_1$, $\ α_2$, …, $\ α_r$线性表示，
      则称$\ α_1$, $\ α_2$, …, $\ α_r$是V的一组基，数r称为V的维数，记作 dim(V)=r，并称V是r维向量空间.

    • 设V是向量空间，$\ α_1$, $\ α_2$, …, $\ α_r$是V的一组基，任给α∈V，若有
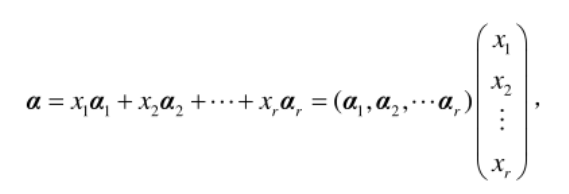
      则称($\ x_1$, $\ x_2$, …, $\ x_r$)为α在基$\ α_1$, $\ α_2$, …, $\ α_r$下的坐标.

  3. 基变换与坐标变换*

向量内积与正交化

  1. 向量的内积

    • 定义：设有n维向量，

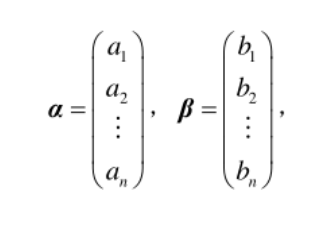
      定义它们的内积为
      〈α,β〉=$\ a1b_1$+ $\ a_2b_2$+ …,+$\ a_nb_n$=$\stackrel{n}{\sum\limits{i=1}}a_ib_i$
      由矩阵乘法，有〈α,β〉=$α^Tβ$=$β^Tα$.
      向量的内积运算满足以下运算律（内积公理）:
      (1) 交换律〈α,β〉=〈β,α〉;
      (2)对加法的分配律〈α,β+γ〉=〈α,β〉+〈α,γ〉:
      (3)对数乘的结合律〈kα,β〉=〈α,kβ)= k〈α,β〉:
      (4）非负性〈α,α)≥0，当且仅当α=0时等号成立.

    • 定义：对于n维向量α=($\ α_1$, $\ α_2$, …, $\ α_n$)$^T$，定义

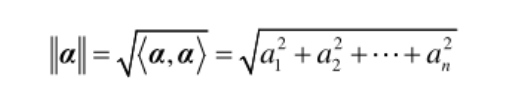
      为向量α的范数（即长度或模）.

      • 定理：向量的范数具有下述性质:
        (1）非负性$||$α$||$≥o;
        (2）齐次性$||$kα$||$=$|$k$|$ $||$α$||$(k为任意实数);
        (3)柯西-施瓦兹(Cauchy-Schwartz）不等式$|$〈α,β〉$|$≤$||$α$||$ $·$ $||$β$||$﹔
        (4）三角不等式:$||$α+β$||$≤$||$α$||$+$||$β$||$.

    • 定义：对n维非零向量α, β ,称

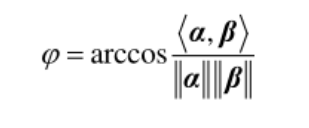
      为向量α，β的夹角.

  2. 向量的正交性

    • 定义：当n维向量α,β满足〈α,β〉= 0时，称α与β正交（或垂直)，记作α⊥β .显然零向量和任何向量都正交，两个非零向量正交当且仅当它们的夹角为$\frac{π}{2}$

      • 定理：向量α 与β正交$\Longleftrightarrow$ $||$α+β$||^2$≤$||$α$||^2$+$||$β$||^2$.
        (勾股定理)

    • 定义：当若干非零向量两两正交时，称它们构成的向量组为正交向量组;进一步地，若它们又都是单位向量，则称为标准正交向量组（或正交规范向量组）.

      • 定理：设$\ α_1$, $\ α_2$, …, $\ α_m$是正交向量组，则$\ α_1$, $\ α_2$, …, $\ α_m$线性无关.

  3. 施密特正交化

    • 定义：若$R^n$的一个基$\ α_1$, $\ α_2$, …, $\ α_n$是一个正交向量组，则称它们是$R^n$的一个正交基，进一步，如果$\ α_1$, $\ α_2$, …, $\ α_n$是标准正交向量组，则称它们是$R^n$的一个标准正交基.

线性方程组的解空间

  1. 齐次线性方程组的基础解系

    • 齐次方程组AX = 0的解向量集合记作

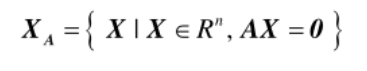
      由于$\overline{A}$=(A$\vdots$ 0)，故恒有$\overline{r}$=r($\overline{A}$)=r(A)=r，也就是说，齐次方程组必定有解，因此解集X$_A$非空，对于解集X$_A$的秩，有如下的重要定理（秩零度定理）：
      对于n元齐次线性方程组AX = 0，系数矩阵的秩和解集的秩满足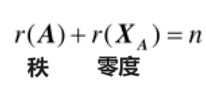

    • 定义：齐次线性方程组AX = 0的解集X$A$的一个极大无关组$\ \xi_1$, $\ \xi_2$, …, $\ \xi{n-r}$称为AX = 0的一个基础解系.
      (特别若r =n，方程组只有唯一零解，从而X$_A$={0}.此时AX = 0没有基础解系，因此R(X$_A$)=0，亦满足R(X$_A$)+R(A)=n)

  2. 齐次线性方程组的解空间

    • 对m×n齐次线性方程组AX = 0，它的解集记作
      X$_A$={X|X∈R$^n$,AX = 0}

    • 对于齐次线性方程组AX = 0，其解具有如下性质:

      • 性质1:若AX$_1$ = 0，AX$_2$ = 0，则A(X$_1$+X$_2$) = 0 .

      • 性质2:若AX$_1$ = 0(k ≠0)，则A(kX$_1$) = 0.

  3. 非齐次线性方程组的解集

    • 非齐次线性方程组AX=β有解时，将它的所有解向量构成的集合称为这个非齐次方程组的解集，记作
      X$_{\overline{A}}$={X|X∈R$^n$,AX=β}
      非齐次方程组AX=β (β≠0）对应的齐次方程组AX=0常常被称为它的导出方程组（简称导出组).

      • 性质1:若AX$_1$ = β，AX$_2$ = β，则A(X$_1$-X$_2$) = 0 .

      • 性质2:若AX$_1$ = β，AX = 0，则A(X$_1$+X$_2$) = β .

    • 定理：设m×n线性方程组AX=β有解，若导出组AX = 0的基础解系为$\ \xi1$, $\ \xi_2$, …, $\ \xi{n-r}$，而$\eta$是AX=β的一特解，则AX=β的通解为