矩阵的初等变换复习
注:本篇适用于复习
初等变换
矩阵的初等变换
求解线性方程组
(对原线性方程组施行的变换可以转换为对增广矩阵的变换)
例:

首元:该行首个非零元且该列唯一非零元
→首变量自由变量
移项(自由变量右移)
补齐
写出通解(线性组合)
定义:下列三种变换称为矩阵的初等行变换(及其逆变换)

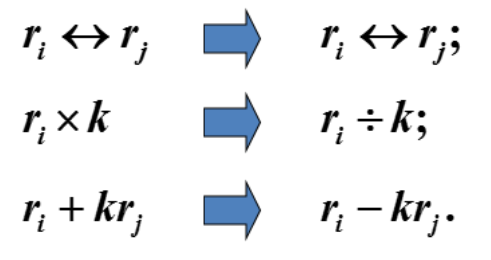
把变换中的r改为c,就是矩阵的初等列变换的定义
矩阵的初等行变换与初等列变换统称为初等变换
矩阵之间的等价关系

若矩阵A经过有限次初等变换变成B,则称矩阵A与B等价(≠相等),记作A↔B
性质:
反身性:A↔A
对称性:若A↔B,则B↔A
传递性:若A↔B, B↔A,则A↔C



初等变换与矩阵乘法的关系
定义:由单位矩阵E经过一次初等变换得到的矩阵称为初等矩阵.三种初等变换对应着三种初等矩阵.
对调单位阵的两行(列);——交换初等阵(初等对换矩阵)
- 由单位矩阵E交换第i行(列)与第j行(列)得到的矩阵
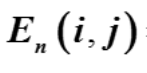
- 由单位矩阵E交换第i行(列)与第j行(列)得到的矩阵
以常数k≠0乘单位阵的某一行(列);——倍乘初等阵(初等倍乘矩阵)
- 由单位矩阵E的第i行(列)乘数k(≠0)得到的矩阵
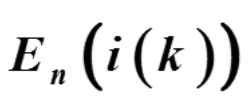
- 由单位矩阵E的第i行(列)乘数k(≠0)得到的矩阵
以k乘单位阵的某一行(列)加到另一行(列) 。——倍加初等阵(初等倍加矩阵)
- 由单位矩阵的第j行乘以数k加到第i行上得到的矩阵(行变换的角度)
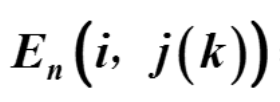
- 由单位矩阵的第j行乘以数k加到第i行上得到的矩阵(行变换的角度)
初等矩阵的逆矩阵
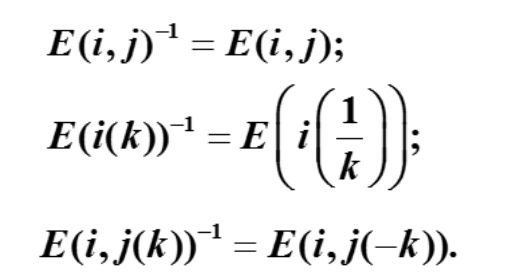
结论

设A是一个m×n矩阵,
对A施行一次初等行变换,相当于在A的左边乘以相应的m阶初等矩阵;
对A施行一次初等列变换,相当于在A的右边乘以相应的n阶初等矩阵.定理
mxn矩阵可以经过若干次初等变换化为如下形式的矩阵:
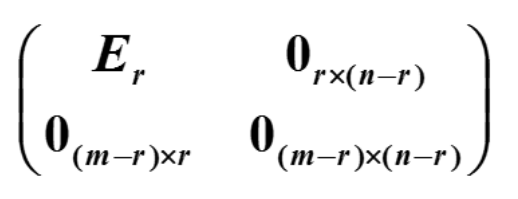
即存在初等矩阵P₁,P₂,…,Ps和Q₁,Q₂,…,Qt使
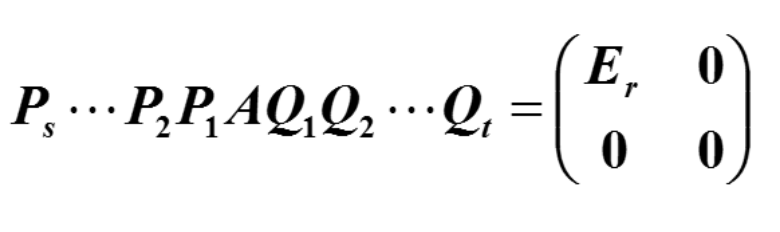
设A为可逆方阵,则A经有限次初等变换可化为单位矩阵,且A可表示成有限个初等矩阵的乘积。
推论1:方阵A可逆的充要条件是
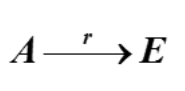
推论2:矩阵A与B等价的充要条件是存在m阶可逆矩阵P及n阶可逆矩阵Q,使PAQ=B.
初等变换的应用
第一个式子用于求解矩阵的逆,第二个式子用于求解AX=B形的方程(均通过行变换实现)
(注意下面的式子都是用等号连接的,式子本身并没有进行初等变换)
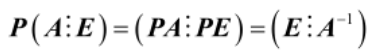
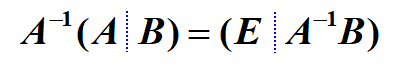
列变换求解XA=B形的方程同理
矩阵的秩
定义
在m×n矩阵A中,任取k行k列(1≤k≤min{m,n}),位于这些行列交叉处的k²个元素,不改变它们在A中所处的位置次序而得的k阶行列式,称为矩阵A的k阶子式.
显然,m×n矩阵的k阶子式共有(mCk*nCk)个.设矩阵A中有一个不等于零的r阶子式D,且所有r +1阶子式(如果存在的话)全等于零,那么D称为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A).
规定:零矩阵的秩等于零.
根据行列式按行(列)展开法则可知,矩阵A中任何一个r +2阶子式(如果存在的话)都可以用r+1阶子式来表示.
如果矩阵A中所有r+1阶子式都等于零,那么所有r+2阶子式也都等于零.
事实上,所有高于r+1阶的子式(如果存在的话)也都等于零.
因此矩阵A的秩就是A中非零子式的最高阶数.
性质
若矩阵A中有某个s阶子式不等于零,则R(A)≥s ;
若矩阵A中所有t阶子式等于零,则R(A)<t 即R(A)≤t-1.若A为n阶矩阵,则A的n阶子式只有一个,即|A|.
当|A|≠0时,R(A)=n ;
可逆矩阵(非奇异矩阵)又称为满秩矩阵.当A=0时,R(A)<n ;
不可逆矩阵(奇异矩阵)又称为降秩矩阵.
若A为m×n矩阵,则0≤R(A)≤min(m, n) .
矩阵转置不改变矩阵的秩(符号打不出来QAQ)
R($\ A^T$) = R(A)
若P、Q可逆,则R(PAQ)= R(A)
若λ≠0,则R(λA)=R(A).
max{R(A),R(B)}≤R(A, B)≤R(A)+R(B) .
特别地,当B=b为非零列向量时,有
R(A)≤R(A,b)≤R(A)+1 .R(A+B)≤R(A)+R(B).(关于“和”)
R(AB)≤min{R(A),R(B)}.(关于“乘”)
若AmxnBnx1=0,则R(A)+R(B)≤n .
计算
定理:矩阵的初等变换不改变矩阵的秩。
推论:若矩阵A与矩阵B等价,则R(A)= R(B).
求矩阵秩的方法:
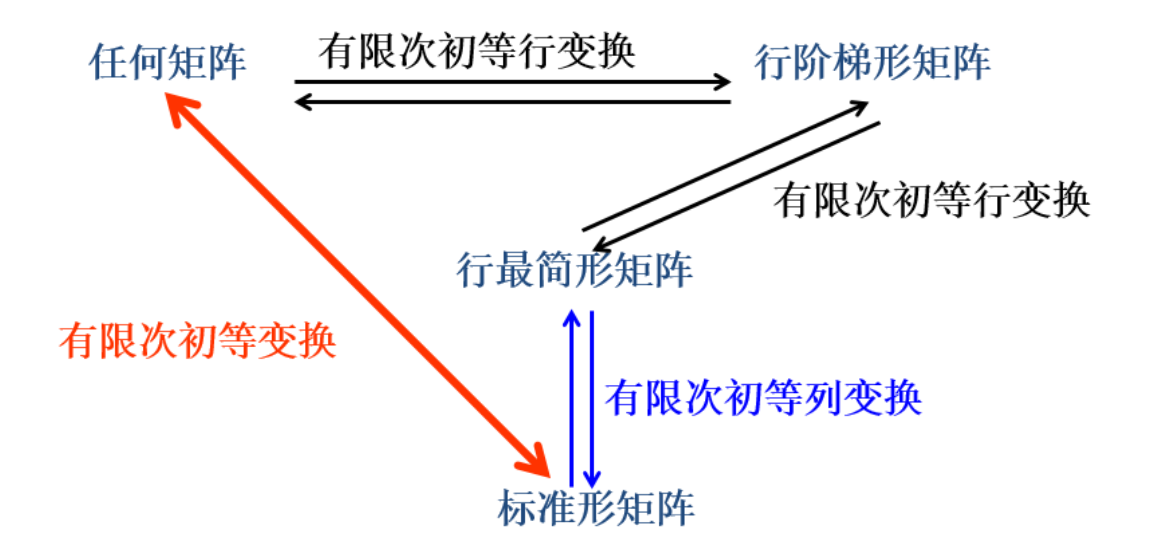
把矩阵用初等行变换化成行阶梯形矩阵,则行阶梯形矩阵中非零行的行数就是原来矩阵的秩.
线性方程组的解
求解
利用初等行变换求解(详细步骤见左边目录1.1)
解的判定
非齐次线性方程AmxnXnx1=bmx1
其系数矩阵为A,增广矩阵为$\overline{A}$,则无解$\Longleftrightarrow$R(A)<R($\overline{A}$);
有唯一解$\Longleftrightarrow$R(A)= R($\overline{A}$)=n ;
推论:当m=n时,有唯一解$\Longleftrightarrow$系数行列式|A|≠0有无穷多解$\Longleftrightarrow$R(A)= R($\overline{A}$)<n
齐次线性方程组
其系数矩阵为A,则只有零解$\Longleftrightarrow$R(A)=n;
有非零解$\Longleftrightarrow$R(A)<n.
推论1:当m<n时,齐次线性方程组必有非零解.
推论2:当m=n时,齐次线性方程组有非零解$\Longleftrightarrow$其系数行列式|A|=0.
齐次线性方程组只有零解$\Longleftrightarrow$其系数行列式|A|≠0.
其他
【精选】Markdown 数学符号大全_markdown数学符号-CSDN博客
使用格式举例:
$\overline{A}$
找矩阵转置的符号没找到采取的是右上角标的形式
$\ A^T$


