注：本篇适用于复习

概念

  1. 定义：由mxn个数排成的m行n列的数表

            对于一般非齐次线性方程组→系数矩阵、增广矩阵（无要求）

loading-ag-254
  1. 特殊矩阵：

  • 零矩阵

  • 行矩阵、列矩阵

  • 方阵

    • 方阵的行列式

  • 上三角形、下三角形矩阵

  • 对角矩阵

    • 数量矩阵（主对角元都相等）(数量矩阵乘矩阵A等于数λ乘矩阵A)

      • 单位矩阵（主对角元都是1）（可以把数乘矩阵转换为矩阵乘法）
  1. 矩阵的相等：行数、列数、对应元素都相等（行列数相等称为同型矩阵）

基本运算

  1. 矩阵的加法

    • 同型才可相加

    • 满足交换律和结合律

    • 负矩阵

  2. 数乘矩阵（数不能与矩阵相加减）

    loading

  3. 矩阵乘法

    • mxs型和sxn型才能相乘→mxn型

    • 结合律、分配律成立，交换律一般不成立（数量矩阵与任何同阶方阵可交换）

    • 消去律一般不成立

    • 两个相乘得0的矩阵可能都不是零矩阵

    • loading

    • （有限个）同阶对角矩阵的乘积

  4. 方阵的乘幂

    • 只有方阵才有乘幂运算

    • 注意矩阵乘法的不可交换性

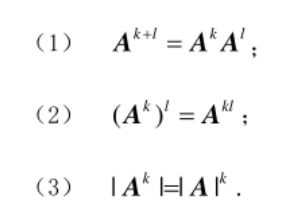
    • loading

  5. 矩阵的转置

    • loading

    • 对称矩阵&反对称矩阵（必为方阵）

逆矩阵

  • 伴随矩阵

    • 代数余子式（行←→列）

    • AA* = A*A = |A|E

  • 逆矩阵（方阵）

    • 若方阵A可逆，则A的逆矩阵是唯一的

    • n阶矩阵A可逆的充分必要条件式|A|≠0（非奇异矩阵）（=0的为奇异矩阵）

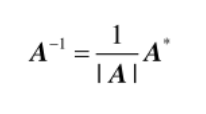
    • 当A可逆时，有loading

    • loading

分块矩阵

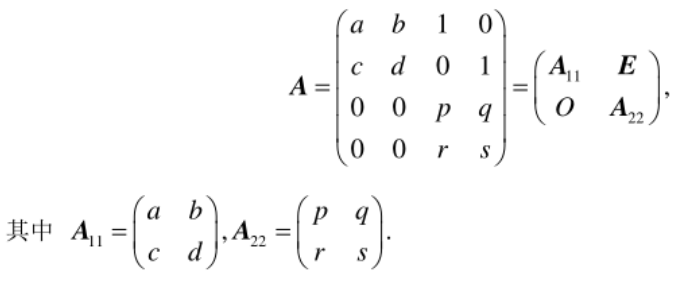
  1. 定义：将矩阵用一些横线和纵线分割成若干个小块，每个小块称为矩阵的子块，以子块为元素的形式上的矩阵称为分块矩阵，（不唯一，与分发有关）如loading

  2. 运算

    • 加法（分块法一致且每块均为同型矩阵）

    • 数乘

    • 乘法（A的列的分发与B的行的分发一致），例

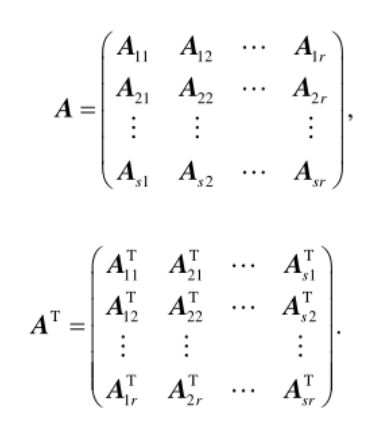
      loading

    • 转置loading

  3. 分块对角矩阵

    • loading

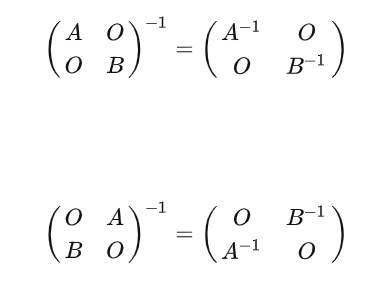
    • 常用结论（待定求解得）loading